- By David Kaiser
- February 07, 2003
- News
Summary
-
The fundamental concepts of servo motion control have not changed significantly in the last 50 years. The basic reasons for using servo systems in contrast to open loop systems include the need to improve transient response times, reduce the steady state errors and reduce the sensitivity to load parameters.

The fundamental concepts of servo motion control have not changed significantly in the last 50 years. The basic reasons for using servo systems in contrast to open loop systems include the need to improve transient response times, reduce the steady state errors and reduce the sensitivity to load parameters.
Improving the transient response time generally means increasing the system bandwidth. Faster response times mean quicker settling allowing for higher machine throughput. Reducing the steady state errors relates to servo system accuracy. Finally, reducing the sensitivity to load parameters means the servo system can tolerate fluctuations in both input and output parameters. An example of an input parameter fluctuation is the incoming power line voltage. Examples of output parameter fluctuations include a real time change in load inertia or mass and unexpected shaft torque disturbances.
Servo control in general can be broken into two fundamental classes of problems. The first class deals with command tracking. It addresses the question of how well does the actual motion follow what is being commanded. The typical commands in rotary motion control are position, velocity, acceleration and torque. For linear motion, force is used instead of torque. The part of servo control that directly deals with this is often referred to as "Feedforward" control. It can be thought of as what internal commands are needed such that the user's motion commands are followed without any error, assuming of course a sufficiently accurate model of both the motor and load is known.
The second general class of servo control addresses the disturbance rejection characteristics of the system. Disturbances can be anything from torque disturbances on the motor shaft to incorrect motor parameter estimations used in the feedforward control. The familiar "P.I.D." (Proportional Integral and Derivative position loop) and "P.I.V." (Proportional position loop Integral and proportional Velocity loop) controls are used to combat these types of problems. In contrast to feedforward control, which predicts the needed internal commands for zero following error, disturbance rejection control reacts to unknown disturbances and modeling errors. Complete servo control systems combine both these types of servo control to provide the best overall performance.
We now examine the two most common forms of disturbance rejection servo control, P.I.D. and P.I.V. After understanding the differences between these two topologies, we then investigate the additional use of a simple feedforward controller for an elementary trapezoidal velocity move profile.
P.I.D. Control
The basic components of a typical servo motion system are depicted in Fig.1 using standard LaPlace notation. In this figure, the servo drive closes a current loop and is modeled simply as a linear transfer function G(s). Of course the servo drive will have peak current limits, so this linear model is not entirely accurate, however it does provide a reasonable representation for our analysis. In their most basic form, servo drives receive a voltage command that represents a desired motor current. Motor shaft torque, T is related to motor current, I by the torque constant, Kt. Equation shows this relationship.
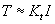
For the purposes of this discussion the transfer function of the current regulator or really the torque regulator can be approximated as unity for the relatively lower motion frequencies we are interested in and therefore we make the following approximation shown in .
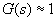
The servomotor is modeled as a lump inertia, J, a viscous damping term, b, and a torque constant, Kt. The lump inertia term is comprised of both the servomotor and load inertia. It is also assumed that the load is rigidly coupled such that the torsional rigidity moves the natural mechanical resonance point well out beyond the servo controller's bandwidth. This assumption allows us to model the total system inertia as the sum of the motor and load inertia for the frequencies we can control. Somewhat more complicated models are needed if coupler dynamics are incorporated.
The actual motor position, q(s) is usually measured by either an encoder or resolver coupled directly to the motor shaft. Again the underlying assumption is that the feedback device is rigidly mounted such that its mechanical resonant frequencies can be safely ignored. External shaft torque disturbances, Td are added to the torque generated by the motor's current to give the torque available to accelerate the total inertia, J.
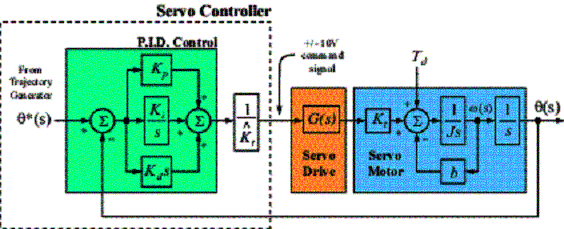
Figure 1. Basic P.I.D. Servo Control Topology.
Around the servo drive and motor block is the servo controller that closes the position loop. A basic servo controller generally contains both a trajectory generator and a P.I.D. controller. The trajectory generator typically provides only position setpoint commands labeled in Fig.1 as q*(s). The P.I.D. controller operates on the position error and outputs a torque command that is sometimes scaled by an estimate of the motor's torque constant, 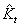 . If the motor's torque constant is not known, the P.I.D. gains are simply re-scaled accordingly. Because the exact value of the motor's torque constant is generally not known, the symbol "^" is used to indicate it is an estimated value in the controller. In general, equation (3) holds with sufficient accuracy so that the output of the servo controller (usually +/-10 volts) will command the correct amount of current for a desired torque.
. If the motor's torque constant is not known, the P.I.D. gains are simply re-scaled accordingly. Because the exact value of the motor's torque constant is generally not known, the symbol "^" is used to indicate it is an estimated value in the controller. In general, equation (3) holds with sufficient accuracy so that the output of the servo controller (usually +/-10 volts) will command the correct amount of current for a desired torque.
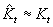
There are three gains to adjust in the P.I.D. controller, Kp, Ki and Kd. These gains all act on the position error defined in . Note the superscript "*" refers to a commanded value.
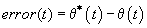
The output of the P.I.D. controller is a torque signal. Its mathematical expression in the time domain is given in .
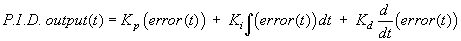
We now look at how one selects the gains, Kp, Ki and Kd.
Tuning the P.I.D. Loop
There are two primary ways to go about selecting the P.I.D. gains. Either the operator uses a trial and error or an analytical approach. Using a trial and error approach relies significantly on the operator's own prior experience with other servo systems. The one significant downside to this is that there is no physical insight into what the gains mean and there is no way to know if the gains are optimum by any definition. However, for decades this was the approach most commonly used. In fact, it is still used today for low performance systems usually found in process control.
To address the need for an analytical approach, Ziegler and Nichols [1] proposed a method based on their many years of industrial control experience. Although they originally intended their tuning method for use in process control, their technique can be applied to servo control. Their procedure basically boils down to these two steps.
Step 1: Set Ki and Kd to zero. Excite the system with a step command. Slowly increase Kp until the shaft position begins to oscillate. At this point, record the value of Kp and set Ko equal to this value. Record the oscillation frequency, fo.
Step 2: Set the final P.I.D. gains using equation .
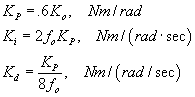
Loosely speaking, the proportional term affects the overall response of the system to a position error. The integral term is needed to force the steady state position error to zero for a constant position command and the derivative term is needed to provide a damping action, as the response becomes oscillatory. Unfortunately all three parameters are inter-related so that by adjusting one parameter will effect any of a previous parameter adjustments.
As an example of this tuning approach, we investigate the response of a Compumotor BE342A motor with a generic servo drive and controller. This servomotor has the following parameters:
Motor Total Inertia J = 50E-6 kgm2
Motor Damping b = .1E-3 Nm/(rad/sec)
Torque Constant Kt = .6 Nm/A
We begin with observing the response to a step input command with no disturbance torque (Td = 0).
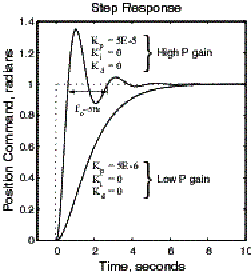
Step 1: Fig. 2a shows the result of slowly increasing only the proportional term. The system begins to oscillate at approximately .5 Hz (fo =.5Hz) with Ko of approximately 5E-5 Nm/rad.
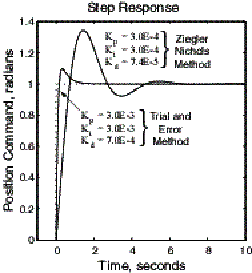
Step 2: Using these values, the optimum P.I.D. gains according to Ziegler-Nichols (Z-N) are then (using equation (6)):
Kp = 3.0E-4 Nm/rad
Ki = 3.0E-4 Nm/(radgsec)
Kd = 7.4E-5 Nm/(rad/sec)
Fig. 2b shows the result of using the Ziegler Nichols gains. The response is somewhat better than just a straight proportional gain. As a comparison, other gains were obtained by trial and error. One set of additional gains is listed in Fig. 2b. Although the trial and error gains gave a faster, less oscillatory response, there is no way of telling if a better solution exits without further exhaustive testing.
a) Determining Ko of Z-N Method
b) Comparing Z-N to Trial and Error Method
Figure 2. Step Response curves for both Ziegler Nichols and Trial and Error Method.
One characteristic that is very apparent in Fig.2 is the length of the settling time. The system using Ziegler Nichols takes about 6 seconds to finally settle making it very difficult to incorporate into any high-performance motion control application. In contrast, the trial and error settings gives a quicker settling time, however no solution was found to completely remove the overshoot.
P.I.V. Control
In order to be able to better predict the system response, an alternative topology is needed. One example of an easier to tune topology is the P.I.V. controller shown in Fig.3. This controller basically combines a position loop with a velocity loop. More specifically, the result of the position error multiplied by Kp becomes a velocity correction command. The integral term, Ki now operates directly on the velocity error instead of the position error as in the P.I.D. case and finally, the Kd term in the P.I.D. position loop is replaced by a Kv term in the P.I.V. velocity loop. Note however, they have the same units, Nm/(rad/sec).
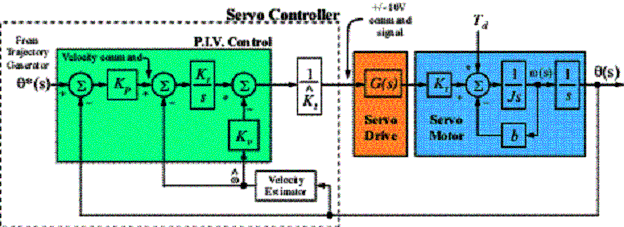
Figure 3. Basic P.I.V. Servo Control Topology.
P.I.V. control requires the knowledge of the motor velocity, labeled velocity estimator in Fig.3. This is usually formed by a simple filter, however significant delays can result and must be accounted for if truly accurate responses are needed. Alternatively, the velocity can be obtained by use of a velocity observer. This observer requires the use of other state variables in exchange for providing zero lag filtering properties. In either case, a clean velocity signal must be provided for P.I.V. control.
As an example of this tuning approach, we investigate the response of a Compumotor Gemini series servo drive and built in controller using the same motor from the previous example. Again, we begin with observing the response to a step input command with no external disturbance torque (Td = 0).
Tuning the P.I.V. Loop
To tune this system, only two control parameters are needed, the bandwidth (BW) and the damping ratio (z). An estimate of the motor's total inertia, ![]() and damping,
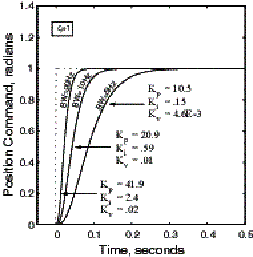
and damping, ![]() are also required at set-up and are obtained using the motor/drive set up utilities. Figure 4 illustrates typical response plots for various bandwidths and damping ratios.
are also required at set-up and are obtained using the motor/drive set up utilities. Figure 4 illustrates typical response plots for various bandwidths and damping ratios.
a) Damping fixed(z=1), Bandwidth varies
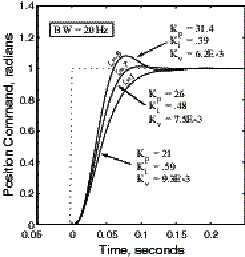
b) Bandwidth fixed(BW=20Hz), Damping varies
Figure 4. Step Response curves for P.I.V. tuning.
With the damping ratio fixed, the bandwidth directly relates to the system rise time as shown in Fig.4 a). The higher the bandwidth, the quicker the rise and settling times. Damping, on the other hand, relates primary to overshoot and secondarily to rise time. The less damping, the higher the overshoot and the slightly quicker the rise time for a fixed bandwidth. This scenario is shown in Fig. 4 b).
The actual internal P.I.V. gains can be calculated directly from the bandwidth and damping values along with the estimates of the inertia, ![]() and motor viscous damping,
and motor viscous damping, ![]() , making their use straightforward and easy to implement. The actual analytical expressions are described in equations - .
, making their use straightforward and easy to implement. The actual analytical expressions are described in equations - .
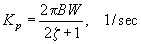
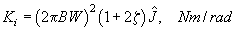
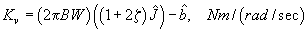
In reality, the user never wants to put a step command into their mechanics, unless of course the step is so small that no damage will result. The use of a step response in determining a system's performance is mostly traditional. The structure of the P.I.V. control and for that matter, the P.I.D. control is designed to reject unknown disturbances to the system. Fig.1 shows this unknown torque disturbance, Td as part of the servo motor model.
Disturbance Rejection Characteristics
If we consider the case where the motor is holding a final position and an unknown disturbance at some frequency is applied to the motor shaft, can we predict how the shaft will respond? To graphically quantify the effect of the P.I.V. gains on this disturbance torque, disturbance rejection plots are drawn showing the magnitude of disturbance needed at a given frequency to result in a specified shaft motion. Fig. 5 illustrates the two cases of constant damping and varying bandwidths (Fig. 5a) and constant bandwidth and varying damping (Fig. 5b).
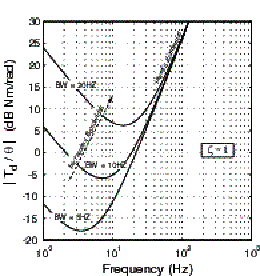
a) Constant Damping (z=1), Bandwidth varies
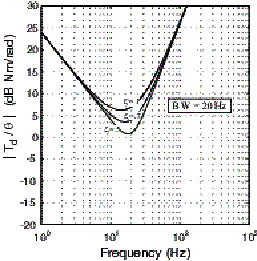
b) Constant Bandwidth (BW=20Hz), Damping varies
Figure 5. Disturbance rejection plots for the P.I.V. system.
In Fig. 5a) the low frequency rejection gain increases as the bandwidth value goes up. Notice for high frequency rejection, only the motor's inertia is effective regardless of the bandwidth of the servo controller. This is why users occasionally request "high inertia" motors even at the expense of requiring more overall torque to make their move. A similar disturbance rejection trend is seen in Fig. 5 b). Here, the mid-frequency rejection gain increases slightly as the damping ratio is raised.
In general the higher the disturbance rejection, the stiffer the system is and the more likely it will provide repeatable moves in the presence of unknown shaft disturbances.
Trapezoidal Motion Profiles
Typically, servo systems are first tuned with a step input in order to get a feel for the system response. Once this is done, the user now is often interested in how their actual motion will behave. At this point, the user must decide on the nature of the velocity profile. By far the most common velocity profile is the trapezoid. This is due to the relative ease of calculating all the state variables needed for motion: position, velocity and acceleration. As the need for smoother accelerations and decelerations becomes greater, either "S" profiles or cubic splines are often employed.
For the purposes of our investigation, we will focus on the use of a simple trapezoidal velocity profile. The test move is 2 revolutions in a quarter of a second, with equal times for acceleration, constant velocity and deceleration. Fig. 6 shows the position and velocity profiles for this move using P.I.V. control. Again notice how by increasing the bandwidth, the position response improves (Fig. 6a) as does the velocity response (Fig. 6 b).
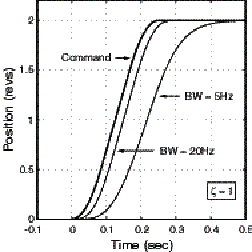
a) Position Response
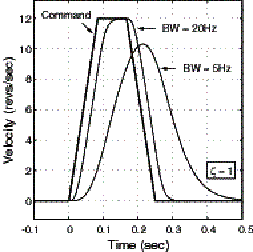
b) Velocity Response
Figure 6. Response Curves using P.I.V. control with z=1 , and varying BW
As a rule of thumb, the bandwidth should be increased as high as possible while still maintaining stable and predictable operation. If some overshoot can be tolerated, the damping ratio can be lowered to further reduce the rise time. Fig. 7 depicts the case where the bandwidth is held constant at 20 Hz and the damping ratio is lowered from 1 (critically damped) to .5 (under damped). Figs. 7 a) and b) show the position and velocity responses respectively. Notice that even with the damping ratio as low as .5, there is very little overshoot. This is because the trapezoidal profile does not greatly excite this damped resonance.
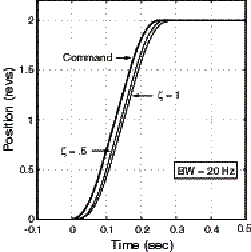
a) Position Response
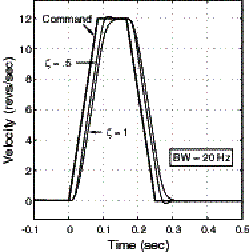
b) Velocity Response
Figure 7. Response Curves using P.I.V. control with BW=20Hz , and varying z
Also notice in Fig.7 the amount of following error in both the position and velocity profiles. The fundamental requirement of any disturbance rejection control is the need to have error in order for the system to respond. Clearly if we want to achieve near zero following error, another solution is needed.
Feedforward Control
In order to achieve near zero following or tracking error, feedforward control is often employed. A requirement for feedforward control is the availability of both the velocity, w*(s) and acceleration, a*(s) commands synchronized with the position commands, q*(s). An example of how feedforward control is used in addition to disturbance rejection control is shown in Fig. 8.
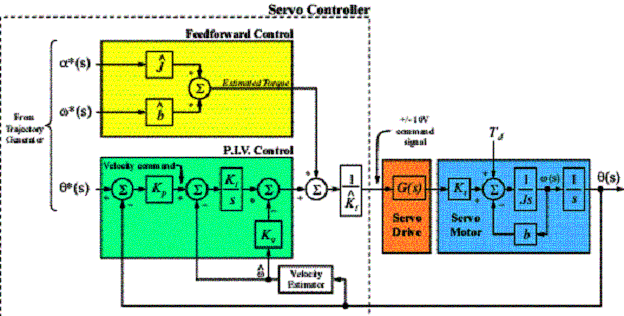
Figure 8. Basic Feedforward and P.I.V. Control Topology.
Feedforward control is used to calculate the required torque needed to make the desired move. The basic equation of motion is given in equation .
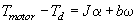
Since the disturbance torque, Td is unknown, the estimated motor torque can only be approximated as shown in equation.
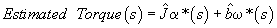
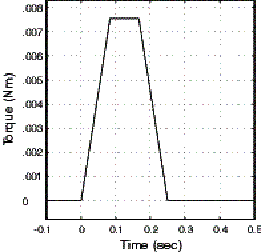
In most cases, the disturbance torque is small enough that estimated torque is very near the required torque. If this is the case, and if the velocity and acceleration commands are available, simple estimates of the total inertia and viscous damping can be used to generate the estimated torque profile in real time without any delay. Continuing with our example, the contributions to the estimated torque by the velocity and acceleration commands are shown in Figs. 9 a) and b) respectively. The composite feedforward signal is shown in Fig. 9 c)
a) Velocity Feedforward = 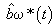
![]()
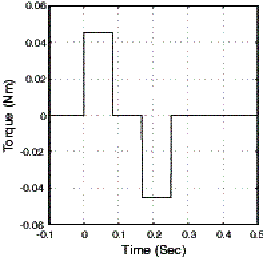
b) Acceleration Feedforward = 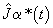
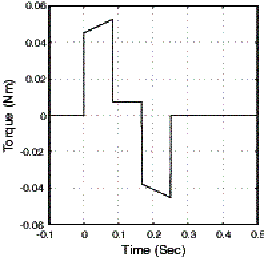
c) Total Feedforward = 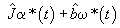
![]()
Figure 9. Estimated Torque Requirements for Trapezoidal Velocity Move Profile
Putting it all together
If we compare the composite feedforward torque signal of Fig. 9 c) with the torque output of only the P.I.V. controller with a bandwidth of 20Hz and a damping ratio of 1, we notice how strikingly similar they are. Fig. 10 shows this comparison. This suggests that we could have near zero following error if our feedforward control is accurate.
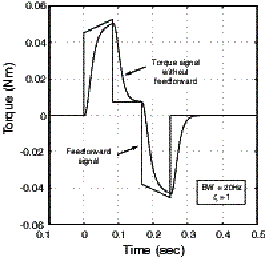
Figure 10. Comparison of Feedforward Torque with the Output of only P.I.V. Control.
Feedforward control goes a long way towards reducing settling times and minimizing overshoot, however there are several of assumptions that ultimately limit its effectiveness. For example, servo amplifiers all have current limits and finite response times. For motion bandwidths in the sub 50 Hz range, the current loops can be safely ignored, however as the need to push the motion bandwidths higher, the current loops need to be accounted for as well. In addition, the single most limiting factor in servo motion control is the resolution and accuracy of the feedback device. Low-resolution encoders contribute to poor velocity estimations that lead to either limit cycling or velocity ripple problems. Finally, compliant couplers that connect the load to the servomotor must also be accounted for as they too limit the useable motion bandwidths.
In summary, disturbance rejection control can be obtained by one of a number of ways, the two most common are P.I.D. and P.I.V. control. The direct use of P.I.D. control can often meet low performance motion control loops and are generally set by either the Ziegler Nichols or by trial and error methods. Overshoot and rise times are tightly coupled making gain adjustments difficult. P.I.V. control on the other hand, provides a method to significantly decouple the overshoot and rise time, allowing for easy set up and very high disturbance rejection characteristics. Finally, feedforward control is needed in addition to disturbance rejection control to minimize the tracking error.
References:
[1] Ziegler, J.G., and Nichols, N.B., Optimum Settings for Automatic Controllers, Transactions of the American Society of Mechanical Engineers (ASME). v. 64, 1942, pgs. 759-768.
About The Author
This article was provided by Parker Compumotor, written by David Kaiser, a Compumotor Staff Engineer. Parker Compumotor is a leader in the motion control industry providing solutions for factory automation needs. They take a system approach to solving your application and build an integrated family of products to match your needs.
Did you enjoy this great article?
Check out our free e-newsletters to read more great articles..
Subscribe

