- By Daniel Muller
- November 23, 2021
- Feature
Summary
When an application requires a reliable, low-cost motor with simple operation, stepper motors can be hard to beat. However, the same straightforward design and driving method that make stepper motors popular can lead to resonance problems in certain conditions.

When an application requires a reliable, low-cost motor with simple operation, stepper motors can be hard to beat. They can be driven step by step without needing an encoder or Hall sensor for rotor position feedback.
However, the same straightforward design and driving method that make stepper motors popular can lead to resonance problems in certain conditions. This article will review different ways to avoid resonance issues and ensure trouble-free motion.
How stepper motors lose synchronization
Stepper motor phases are commutated sequentially by an external electronic driver that subsequently moves the rotor—which often carries a permanent magnet—from one stable position to the next. An appropriate motor will provide a sufficient torque to move the rotor and load to the next step after each commutation. If the torque is not sufficient or if the speed is too high, the synchronization between the driver and the actual rotor position can be lost.

Figure 1 shows the concept of a very simple two-phase stepper motor with one pole pair. The electronically driven commutation sequence (A, B, -A, -B) will create a full rotor revolution over four steps, at 90 degrees per step.
Oscillation around stable position
At each step, the rotor tends to align its poles with the stator’s poles. As long as one phase is energized continuously—without switching to the next phase—the rotor holds a stable position.

Figure 2 shows that if the rotor moves ahead of the target position, the motor will develop a negative torque that generally pulls the rotor back to the target position. Conversely, when the rotor is before the target position, a positive torque will push the rotor forward in the direction of the target position. In these conditions, an oscillation phenomenon can easily occur, as the combined rotor inertia and inertia of the load, if any, will prevent the rotor from stopping exactly on the stable position. When the rotor moves from a stable position to the next stable position in the succeeding step, the angular position will usually overshoot the rotor’s target position due to the kinetic energy that the rotor carries during its approach. It will then begin to oscillate around the position as soon as the negative torque draws the rotor back to the target position. The natural frequency of this periodic oscillation can be calculated as follows:
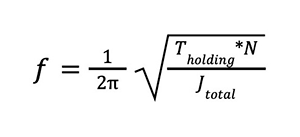
Tholding: Holding torque (Nm)
N: Number of pole pairs
Jtotal: Total moment of inertia (Jrotor+Jload)
System losses will cause this oscillation to reduce in magnitude over time. This amplitude reduction is usually referred to as “damping” and depends on several factors. Eventually, the damping will always bring the rotor to a still position if only one phase is energized. However, sometimes it makes sense to optimize the damping when the phases are energized sequentially.

At high speed, the commutation becomes more frequent. If the oscillation does not end before the next step is commanded, there is a risk of resonance—the tendency of the mechanical system to respond at a greater amplitude. This will likely happen if the commutation frequency is close to the system’s natural frequency, as seen in Figure 3.
Resonance can lead to erratic operation of the motor, loss of steps and random changes to its rotational direction. We recommend you take preventive measures to avoid resonance and ensure proper synchronicity between the command and the actual position.
Strategies to prevent resonance
Avoid natural frequency
Resonance typically occurs when the commutation frequency is close to the mechanical system’s natural vibration frequency. Accordingly, the most basic way to prevent the occurrence of resonance is to keep the commutation frequency away from the system’s natural frequency. Working with a different commutation frequency can require other changes in the application in order to keep the same speed, but such changes are not always possible.
Shift natural frequency
Instead of changing the commutation frequency, you can shift the natural frequency higher or lower, based on your constraints or challenges, in order to prevent the commutation frequency from matching it. This can be done by working on the two factors that influence the natural frequency: the holding torque and the total inertia in the system.
- Holding torque: A motor is typically sized to be used at its rated current, which defines the holding torque. Using a higher current to increase the holding torque is not possible for a continuous operation because the higher joule losses produce an excessive coil temperature. However, a lower current can be used to achieve a lower holding torque and to shift the natural frequency down if the lower torque can meet the application’s needs.
- Inertia. Because the mechanical system’s moment of inertia is the sum of the motor’s rotor inertia plus the load inertia, design changes can alter the rotor’s inertia. For example, the natural resonance frequency of a motor without load is generally provided in the motor’s specifications. Otherwise, the user can work on the load inertia completely independent from the motor. Increasing the inertia will shift the overall system’s natural frequency down, and vice-versa. Changing the system’s inertia can also affect the motor’s performance in the application, so be sure to consult with your motor provider to ensure proper operation.
Prevent resonance with microstepping
The higher the energy brought into the mechanical system, the higher the risk to trigger a resonance phenomenon. To prevent this, microstepping can be a good alternative to driving a stepper motor with full steps. Each microstep has a smaller step angle and requires less energy to move from one stable position to the next. Because the target position overshoot is smaller along with the magnitude of the oscillation, microstepping is often an effective way to avoid resonance. In addition, microsteps generally offer lower noise, less vibration and smoother operation.
Damping via friction
Friction provides a braking torque that is opposed to the instant direction of rotation. This torque is constant, regardless of motor speed. While it helps dampen the oscillation and prevents resonance, keep in mind that friction also adds to the load applied on the motor at any speed. Therefore, it is important to ensure that the motor provides sufficient performance when adding friction to prevent resonance.
Viscous friction also provides a braking torque, but its magnitude depends on the motor speed. The higher the speed, the stronger the viscous damping. For this reason, viscous damping provides strong braking at the beginning while the speed and oscillation amplitude are greater and only very light braking once the oscillation is smaller—unlike dry friction which provides the same braking magnitude even at very low speed. That makes viscous friction desirable for oscillation damping within a very short time and without adding too much load onto the motor.
Different phenomena can bring viscous friction into a system:
- Eddy currents. Transient currents induced in the stator, also known as iron losses, act as a braking torque. These losses can be considered viscous friction because they are higher when speed is higher, and they do not exist without motion. Depending on the motor design and technology, iron losses can be different from one motor to another. Disk magnet motors, for example, usually have limited iron losses and are able to reach relatively high speeds. Therefore, designers should not rely on iron losses alone to dampen the oscillation of a disk magnet motor but also consider another method of preventing resonance when using such a motor.
- Back-EMF. When induced in the coil, back-EMF voltage can produce a current and a braking torque that will dampen the oscillation. This current is typically allowed when the unenergized phase is short-circuited, and it is also proportional to the motor speed. Since higher speeds create a stronger braking torque, it can also be considered a viscous friction. Chopper drivers typically do not allow this type of damping since the current is kept constant despite back-EMF variations.
- Electronic damping. These methods can be applied by driving the motor in a particular way without changing any mechanical properties in the system.
- An external mechanical damper. This type of device can also be added in the application or onto the motor to absorb some of the vibration energy that can cause resonance.
Your motor provider can help eliminate resonance trouble spots
While stepper motors offer easy and cost-effective positioning, their step-by-step, sequential operation can lead to resonance issues under certain conditions. Sometimes the resonance can be solved by acting on a single cause. But, depending on the motor technology and design, there may be additional frequency ranges such as mid-frequency resonance that can trigger resonance, apart from natural oscillation frequency. Motor providers can help you determine the frequency ranges that are likely to trigger resonance and offer solutions to prevent the issues from occurring.
For more information about Portescap stepper motors, visit our product page.
About The Author
Daniel Muller is an application engineer at Portescap.
Did you enjoy this great article?
Check out our free e-newsletters to read more great articles..
Subscribe

